Survival Data • simstudy

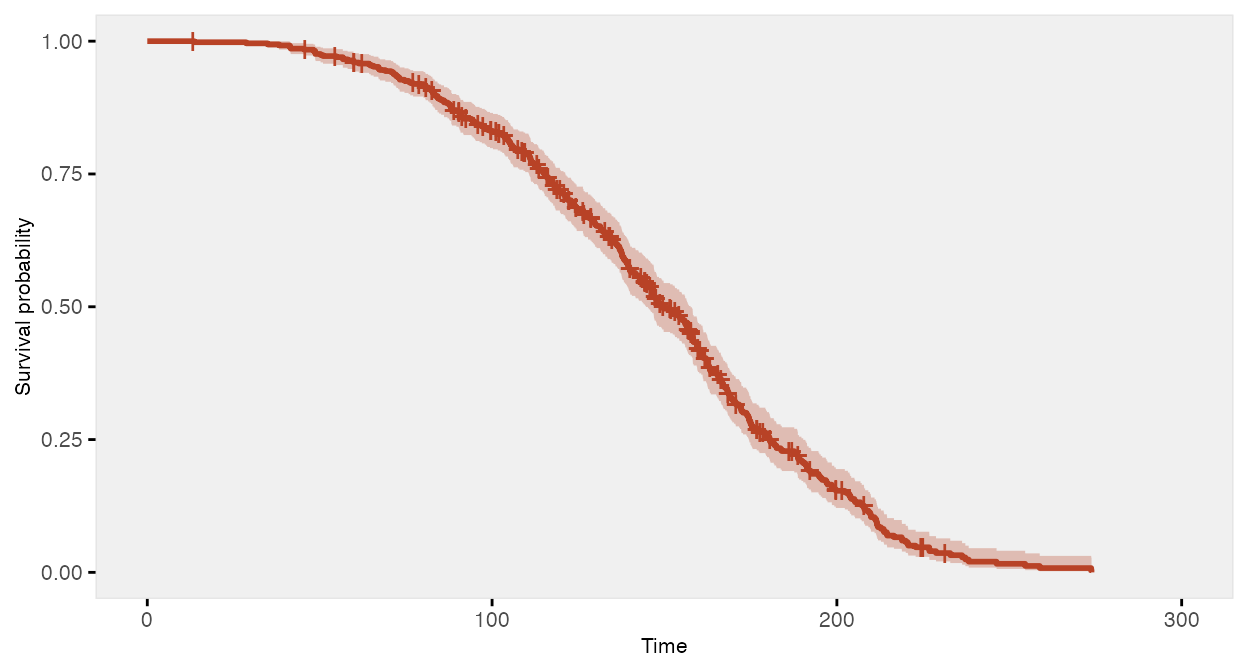
Time-to-event data, including both survival and censoring times, are created using functions defSurv and genSurv. The survival data definitions require a variable name as well as a specification of a scale value, which determines the mean survival time at a baseline level of covariates (i.e. all covariates set to 0). The Weibull distribution is used to generate these survival times. In addition, covariates (which have been defined previously) that influence survival time can be included in the formula field. Positive coefficients are associated with longer survival times (and lower hazard rates). Finally, the shape of the distribution can be specified. A shape value of 1 reflects the exponential distribution. As of simstudy version 0.5.0, it is also possible to generate survival data that violate a proportional hazards assumption. In addition, data with two or more competing risks can be generated.

Weibull distribution

The density, mean, and variance of the Weibull distribution that is used in the data generation process are defined by the parameters $\lambda$ (scale) and $\nu$ (shape) as shown below.

\begin{aligned} f(t) &= \frac{t^{\frac{1}{\nu}-1}}{\lambda \nu} exp\left(-\frac{t^\frac{1}{\nu}}{\lambda}\right) \\ E(T) &= \lambda ^ \nu \Gamma(\nu + 1) \\ Var(T) &= (\lambda^2)^\nu \left( \Gamma(2 \nu + 1) - \Gamma^2(\nu + 1) \right) \\ \end{aligned}

The survival time $T$ data are generated based on this formula:

$T = \left( -\frac{log(U) \lambda}{exp(\beta ^ \prime x)} \right)^\nu,$

where $U$ is a uniform random variable between 0 and 1, $\beta$ is a vector of parameters in a Cox proportional hazard model, and $x$ is a vector of covariates that impact survival time. $\lambda$ and $\nu$ can also vary by covariates.

Generating standard survival data with censoring

Here is an example showing how to generate data with covariates. In this case the scale and shape parameters will vary by group membership.

# Baseline data definitions

def <- defData(varname = "x1", formula = 0.5, dist = "binary")
def <- defData(def, varname = "grp", formula = 0.5, dist = "binary")

# Survival data definitions

set.seed(282716)

sdef <- defSurv(varname = "survTime", formula = "1.5*x1", scale = "grp*50 + (1-grp)*25",
    shape = "grp*1 + (1-grp)*1.5")
sdef <- defSurv(sdef, varname = "censorTime", scale = 80, shape = 1)

sdef

## Key: <varname>
##       varname formula               scale               shape transition
##        <char>  <char>              <char>              <char>      <num>
## 1: censorTime       0                  80                   1          0
## 2:   survTime  1.5*x1 grp*50 + (1-grp)*25 grp*1 + (1-grp)*1.5          0

The data are generated with calls to genData and genSurv:

# Baseline data definitions

dtSurv <- genData(300, def)
dtSurv <- genSurv(dtSurv, sdef)

head(dtSurv)

## Key: <id>
##       id    x1   grp censorTime survTime
##    <int> <int> <int>      <num>    <num>
## 1:     1     0     0     42.923    9.875
## 2:     2     0     1     77.166   17.338
## 3:     3     0     1    143.773  142.939
## 4:     4     1     1    181.853   16.470
## 5:     5     1     0    210.939  108.276
## 6:     6     0     1     34.096    8.122

# A comparison of survival by group and x1

dtSurv[, round(mean(survTime), 1), keyby = .(grp, x1)]

## Key: <grp, x1>
##      grp    x1    V1
##    <int> <int> <num>
## 1:     0     0 149.2
## 2:     0     1  23.4
## 3:     1     0  46.3
## 4:     1     1  12.2

Observed survival times and censoring indicators can be generated using the competing risk functionality and specifying a censoring variable:

dtSurv <- genData(300, def)
dtSurv <- genSurv(dtSurv, sdef, timeName = "obsTime", censorName = "censorTime",
    eventName = "status", keepEvents = TRUE)

head(dtSurv)

## Key: <id>
##       id    x1   grp censorTime survTime obsTime status       type
##    <int> <int> <int>      <num>    <num>   <num>  <num>     <char>
## 1:     1     0     1     92.368   49.071  49.071      1   survTime
## 2:     2     1     0     45.801   25.639  25.639      1   survTime
## 3:     3     1     1    278.210    4.045   4.045      1   survTime
## 4:     4     0     0     12.663   13.325  12.663      0 censorTime
## 5:     5     0     0     26.531  323.764  26.531      0 censorTime
## 6:     6     1     0     23.514    0.157   0.157      1   survTime

# estimate proportion of censoring by x1 and group

dtSurv[, round(1 - mean(status), 2), keyby = .(grp, x1)]

## Key: <grp, x1>
##      grp    x1    V1
##    <int> <int> <num>
## 1:     0     0  0.71
## 2:     0     1  0.10
## 3:     1     0  0.44
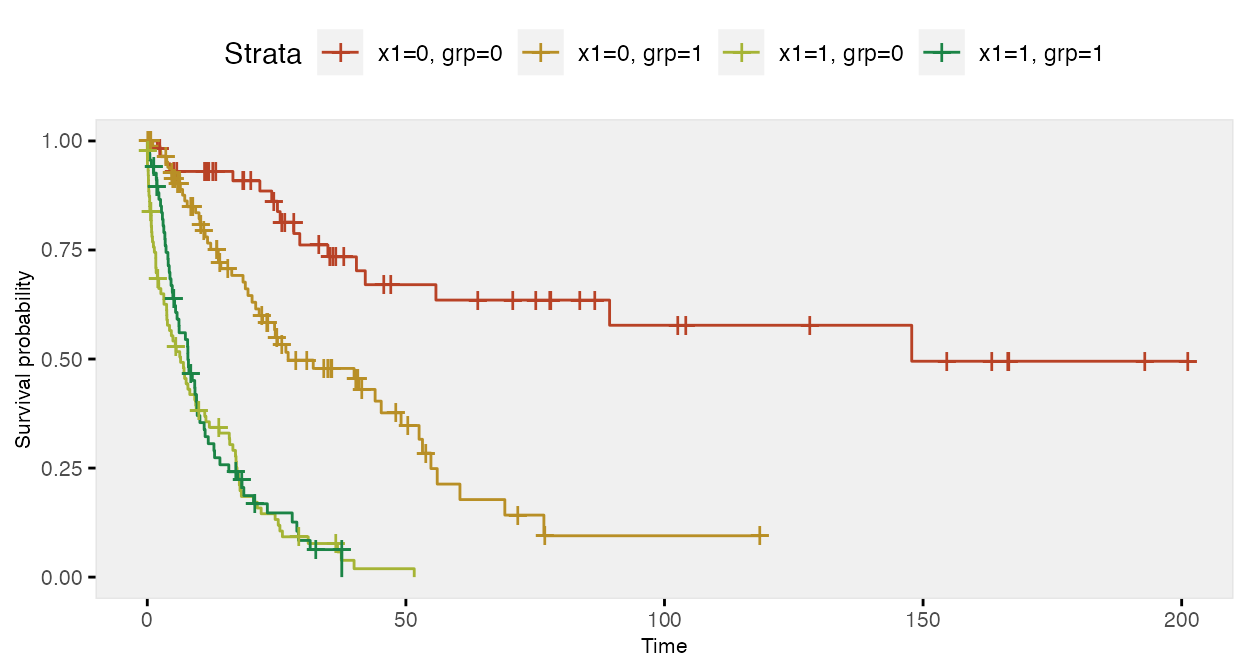
## 4:     1     1  0.13

Here is a Kaplan-Meier plot of the data by the four groups:

Here is a survival analysis (using a Cox proportional hazard model) of a slightly simplified data set with two baseline covariates only:

# Baseline data definitions

def <- defData(varname = "x1", formula = 0.5, dist = "binary")
def <- defData(def, varname = "x2", formula = 0.5, dist = "binary")

# Survival data definitions

sdef <- defSurv(varname = "survTime", formula = "1.5*x1 - .8*x2", scale = 50, shape = 1/2)
sdef <- defSurv(sdef, varname = "censorTime", scale = 80, shape = 1)

dtSurv <- genData(300, def)
dtSurv <- genSurv(dtSurv, sdef, timeName = "obsTime", censorName = "censorTime",
    eventName = "status")

coxfit <- survival::coxph(Surv(obsTime, status) ~ x1 + x2, data = dtSurv)

The 95% confidence intervals of the parameter estimates include the values used to generate the data:

Characteristic	log(HR)¹	95% CI¹
x1	1.5	1.2, 1.8
x2	-0.89	-1.1, -0.64
¹ HR = Hazard Ratio, CI = Confidence Interval

Competing risks

In the previous example, we actually used the competing risk mechanism in genSurv to generate an observed time variable (which was the earliest of the censoring and event time). This is done by specifying a timeName argument that will represent the observed time value. The event status is indicated in the field set by the eventName argument (which defaults to “event”). If a variable name is indicated in the censorName argument, the censored events automatically have a value of 0. As we saw above, competing risk information can be generated as part of genSurv. However, there is an additional function addCompRisk that will generate the competing risk information using an existing data set. The example here will take that approach.

d1 <- defData(varname = "x1", formula = .5, dist = "binary")
d1 <- defData(d1, "x2", .5, dist = "binary")

dS <- defSurv(varname = "event_1", formula = "-10 - 0.6*x1 + 0.4*x2", shape = 0.3)
dS <- defSurv(dS, "event_2", "-6.5 + 0.3*x1 - 0.5*x2", shape = 0.5)
dS <- defSurv(dS, "censor", "-7", shape = 0.55)

dtSurv <- genData(1001, d1)
dtSurv <- genSurv(dtSurv, dS)

dtSurv

## Key: <id>
##          id    x1    x2  censor event_1 event_2
##       <int> <int> <int>   <num>   <num>   <num>
##    1:     1     0     1  39.655  17.777  23.618
##    2:     2     1     0 101.140  24.092  32.411
##    3:     3     1     0  13.181  40.485  36.503
##    4:     4     0     0  26.969  18.084  45.124
##    5:     5     0     1  15.320  14.174  37.962
##   ---                                          
##  997:   997     0     0   7.035  16.535  28.583
##  998:   998     0     0  25.293  19.838  51.290
##  999:   999     0     0  45.005  14.887  29.274
## 1000:  1000     1     0  11.105  15.367   7.779
## 1001:  1001     1     0  69.181  24.303  18.322

dtSurv <- addCompRisk(dtSurv, events = c("event_1", "event_2", "censor"), 
            timeName = "time", censorName = "censor")
dtSurv

## Key: <id>
## Index: <type>
##          id    x1    x2   time event    type
##       <int> <int> <int>  <num> <num>  <char>
##    1:     1     0     1 17.777     1 event_1
##    2:     2     1     0 24.092     1 event_1
##    3:     3     1     0 13.181     0  censor
##    4:     4     0     0 18.084     1 event_1
##    5:     5     0     1 14.174     1 event_1
##   ---                                       
##  997:   997     0     0  7.035     0  censor
##  998:   998     0     0 19.838     1 event_1
##  999:   999     0     0 14.887     1 event_1
## 1000:  1000     1     0  7.779     2 event_2
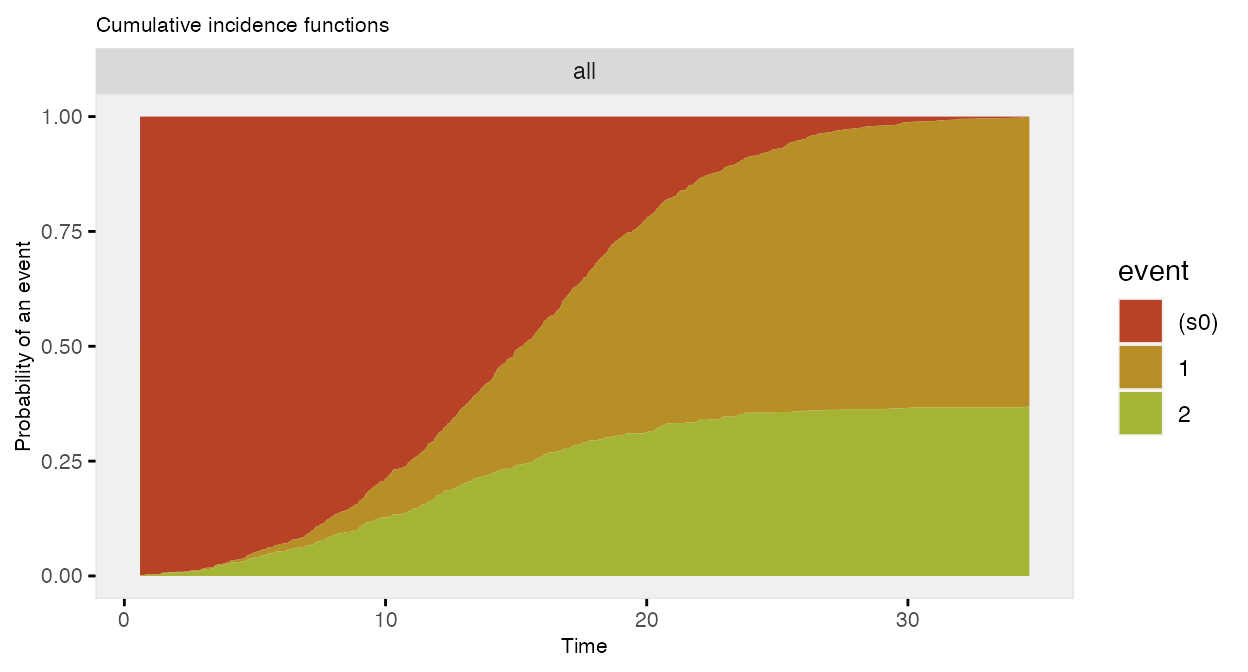
## 1001:  1001     1     0 18.322     2 event_2

The competing risk data can be plotted using the cumulative incidence functions (rather than the survival curves):

The data generation can all be done in two (instead of three) steps:

dtSurv <- genData(101, d1)
dtSurv <- genSurv(dtSurv, dS, timeName = "time", censorName = "censor")
dtSurv

## Key: <id>
## Index: <type>
##         id    x1    x2   time event    type
##      <int> <int> <int>  <num> <num>  <char>
##   1:     1     0     1 11.929     1 event_1
##   2:     2     0     0 20.427     1 event_1
##   3:     3     1     1 14.487     2 event_2
##   4:     4     1     0 12.219     2 event_2
##   5:     5     1     1 16.602     1 event_1
##  ---                                       
##  97:    97     1     1 17.890     2 event_2
##  98:    98     1     0 15.838     2 event_2
##  99:    99     1     1 20.176     1 event_1
## 100:   100     0     0 20.244     1 event_1
## 101:   101     1     0 14.887     1 event_1

Introducing non-proportional hazards

In the standard simstudy data generation process for survival/time-to-event outcomes that includes covariates that effect the hazard rate at various time points, the ratio of hazards comparing different levels of a covariate are constant across all time points. For example, if we have a single binary covariate $x$ , the hazard $\lambda(t)$ at time $t$ is

$\lambda(t|x) = \lambda_0(t) e ^ {\beta x}$ where $\lambda_0(t)$ is a baseline hazard when $x=0$ . The ratio of the hazards for $x=1$ compared to $x=0$ is

$\frac{\lambda_0(t) e ^ {\beta}}{\lambda_0(t)} = e ^ \beta,$

so the log of the hazard ratio is a constant $\beta$ , and the hazard ratio is always $e^\beta$ .

However, we may not always want to make the assumption that the hazard ratio is constant over all time periods. To facilitate this, it is possible to specify two different data definitions for the same outcome, using the transition field to specify when the second definition replaces the first. (While it would theoretically be possible to generate data for more than two periods, the process is more involved, and has not been implemented at this time.)

Constant/proportional hazard ratio

To start, here is an example assuming a constant log hazard ratio of -0.7:

def <- defData(varname = "x", formula = 0.4, dist = "binary")

defS <- defSurv(varname = "death", formula = "-14.6 - 0.7*x", shape = 0.35)
defS <- defSurv(defS, varname = "censor", scale = exp(13), shape = 0.5)

dd <- genData(500, def)
dd <- genSurv(dd, defS, digits = 2, timeName = "time", censorName = "censor")

fit <- survfit(Surv(time, event) ~ x, data = dd)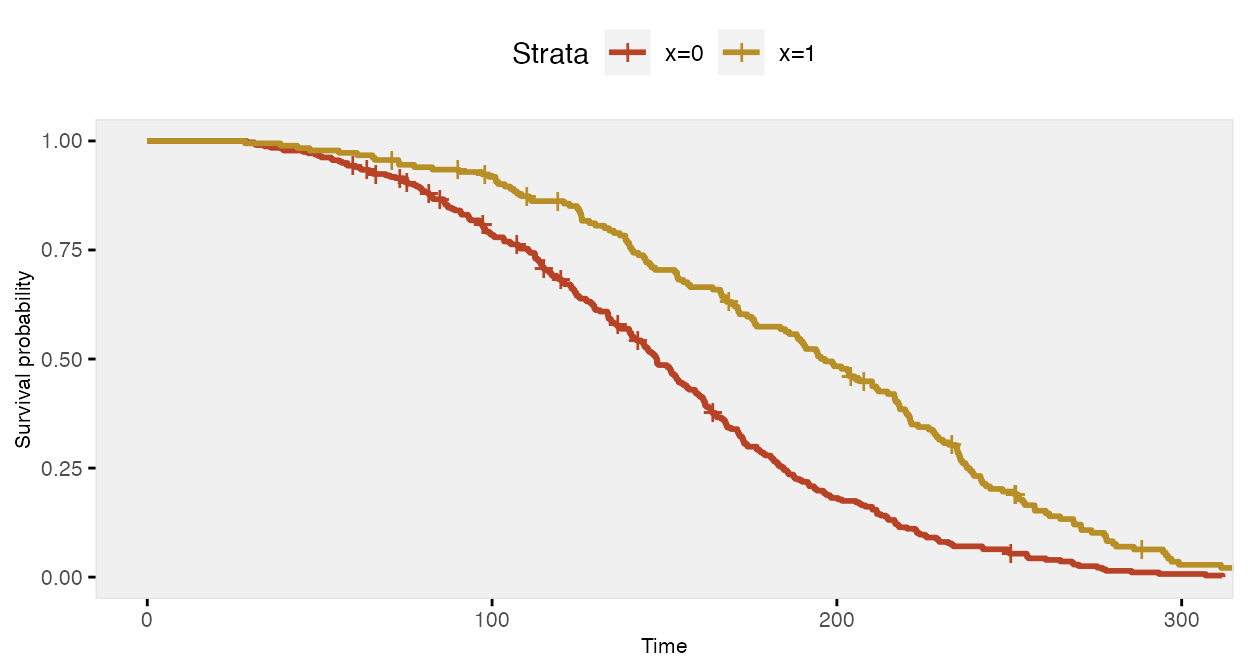

The Cox proportional hazards model recovers the correct log hazards rate:

coxfit <- coxph(formula = Surv(time, event) ~ x, data = dd)

Characteristic	log(HR)¹	95% CI¹	p-value
x	-0.69	-0.88, -0.50
¹ HR = Hazard Ratio, CI = Confidence Interval

We can test the assumption of proportional hazards using weighted residuals. If the $\text{p-value} < 0.05$ , then we would conclude that the assumption of proportional hazards is not warranted. In this case $p = 0.22$ , so the model is apparently reasonable:

cox.zph(coxfit)

##        chisq df    p
## x       2.61  1 0.11
## GLOBAL  2.61  1 0.11

Non-constant/non-proportional hazard ratio

In this next case, the risk of death when $x=1$ is lower at all time points compared to when $x=0$ , but the relative risk (or hazard ratio) changes at 150 days:

def <- defData(varname = "x", formula = 0.4, dist = "binary")

defS <- defSurv(varname = "death", formula = "-14.6 - 1.3*x", shape = 0.35, transition = 0)
defS <- defSurv(defS, varname = "death", formula = "-14.6 - 0.4*x", shape = 0.35,
    transition = 150)
defS <- defSurv(defS, varname = "censor", scale = exp(13), shape = 0.5)

dd <- genData(500, def)
dd <- genSurv(dd, defS, digits = 2, timeName = "time", censorName = "censor")

fit <- survfit(Surv(time, event) ~ x, data = dd)

The survival curve for the sample with $x=1$ has a slightly different shape under this data generation process compared to the previous example under a constant hazard ratio assumption; there is more separation early on (prior to day 150), and then the gap is closed at a quicker rate.

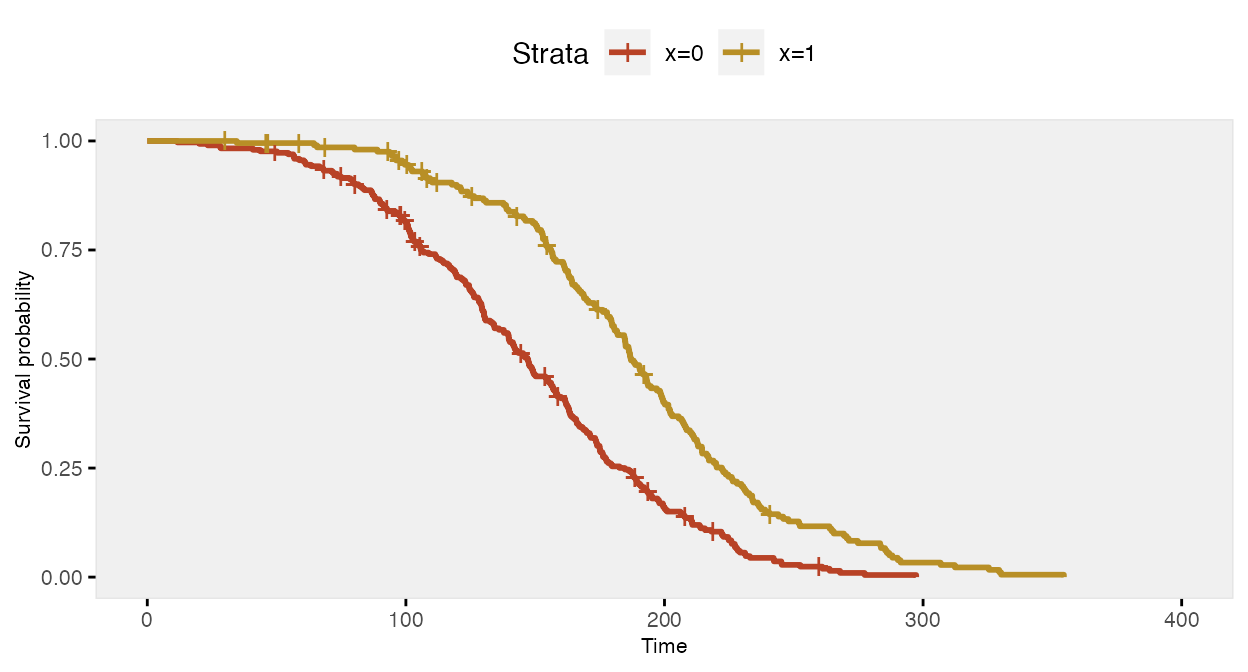
If we ignore the possibility that there might be a different relationship over time, the Cox proportional hazards model gives an estimate of the log hazard ratio quite close to -0.70:

coxfit <- survival::coxph(formula = Surv(time, event) ~ x, data = dd)

Characteristic	log(HR)¹	95% CI¹	p-value
x	-0.72	-0.91, -0.52
¹ HR = Hazard Ratio, CI = Confidence Interval

However, further inspection of the proportionality assumption should make us question the appropriateness of the model. Since $p<0.05$ , we would be wise to see if we can improve on the model.

cox.zph(coxfit)

##        chisq df      p
## x       9.26  1 0.0023
## GLOBAL  9.26  1 0.0023

We might be able to see from the plot where proportionality diverges, in which case we can split the data set into two parts at the identified time point. (In many cases, the transition point or points won’t be so obvious, in which case the investigation might be more involved.) By splitting the data at day 150, we get the desired estimates:

dd2 <- survSplit(Surv(time, event) ~ ., data= dd, cut=c(150),
                 episode= "tgroup", id="newid")

coxfit2 <- survival::coxph(Surv(tstart, time, event) ~ x:strata(tgroup), data=dd2)

Characteristic	log(HR)¹	95% CI¹	p-value
x * strata(tgroup)
x * tgroup=1	-1.3	-1.7, -0.94
x * tgroup=2	-0.40	-0.65, -0.16	0.001
¹ HR = Hazard Ratio, CI = Confidence Interval

And the diagnostic test of proportionality confirms the appropriateness of the model:

cox.zph(coxfit2)

##                  chisq df    p
## x:strata(tgroup)  0.57  2 0.75
## GLOBAL            0.57  2 0.75

Generating parameters for survival distribution

Throughout this vignette, I have been using various assumptions for the parameters - formula, scale, and shape - that define the Weibull-based survival distribution. Where do these assumptions come from and how can we determine what is appropriate to use in our simulations? That will depend, of course, on each specific application and use of the simulation, but there are two helper functions in simstudy, survGetParams and survParamPlot, that are intended to guide the process.

survGetParams will provide the formula and shape parameters (the scale parameter will always be set to 1) that define a curve close to points provided as inputs. For example, if we would like to find the parameters for a distribution where 80% survive until day 100, and 10% survive until day 200 (any number of points may be provided):

points <- list(c(100, 0.80), c(200, 0.10))
r <- survGetParams(points)
r

## [1] -17.0065167   0.2969817

We can visualize the curve that is defined by these parameters:

survParamPlot(f = r[1], shape = r[2], points)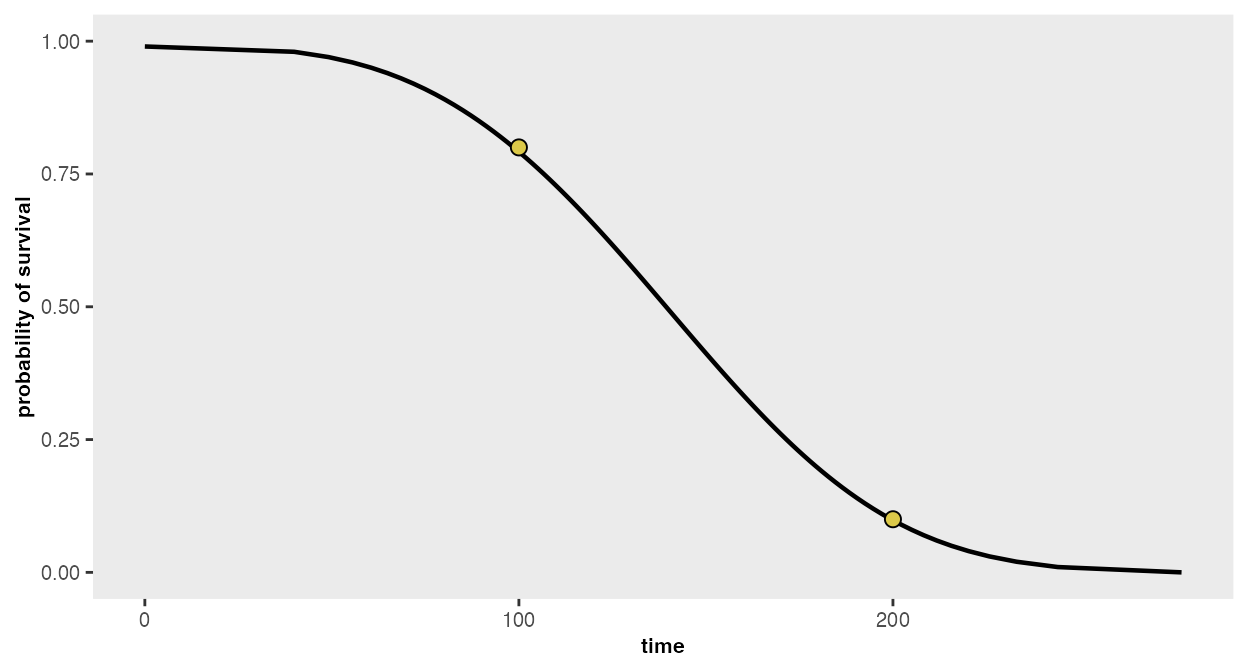

And we can generate data based on these parameters:

defS <- defSurv(varname = "death", formula = -17, scale = 1, shape = 0.3)
defS <- defSurv(defS, varname = "censor", formula = 0, scale = exp(18.5), shape = 0.3)

dd <- genData(500)
dd <- genSurv(dd, defS, timeName = "time", censorName = "censor")