Custom distributions can be specified in defData and
defDataAdd by setting the argument dist to
“custom”. When defining a custom distribution, you provide the name of
the user-defined function as a string in the formula argument.
The arguments of the custom function are listed in the variance
argument, separated by commas and formatted as “arg_1 =
val_form_1, arg_2 = val_form_2,
,
arg_K = val_form_K”.
Here, the arg_k’s represent the names of the arguments
passed to the customized function, where
ranges from
to
.
You can use values or formulas for each val_form_k. If formulas
are used, ensure that the variables have been previously generated.
Double dot notation is available in specifying value_formula_k.
One important requirement of the custom function is that the parameter
list used to define the function must include an argument”n =
n”, but do not include
in the definition as part of defData or
defDataAdd.
Example 1
Here is an example where we would like to generate data from a
zero-inflated beta distribution. In this case, there is a user-defined
function zeroBeta that takes on shape parameters
and
,
as well as
,
the proportion of the sample that is zero. Note that the function also
takes an argument
that will not to be be specified in the data definition;
will represent the number of observations being generated:
zeroBeta <- function(n, a, b, p0) {
betas <- rbeta(n, a, b)
is.zero <- rbinom(n, 1, p0)
betas*!(is.zero)
}The data definition specifies a new variable that sets and to 0.75, and :
def <- defData(
varname = "zb",
formula = "zeroBeta",
variance = "a = 0.75, b = 0.75, p0 = 0.02",
dist = "custom"
)The data are generated:
## Key: <id>
## id zb
## <int> <num>
## 1: 1 0.93922887
## 2: 2 0.35609519
## 3: 3 0.08087245
## 4: 4 0.99796758
## 5: 5 0.28481522
## ---
## 99996: 99996 0.81740836
## 99997: 99997 0.98586333
## 99998: 99998 0.68770216
## 99999: 99999 0.45096868
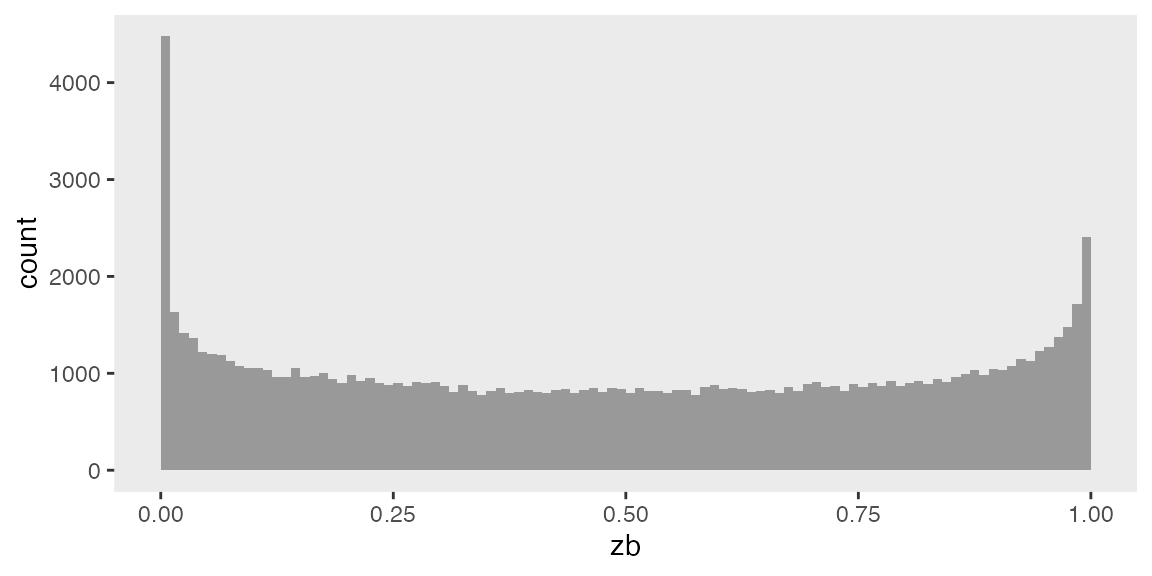
## 100000: 100000 0.74101272A plot of the data reveals dis-proportion of zero’s:
Example 2
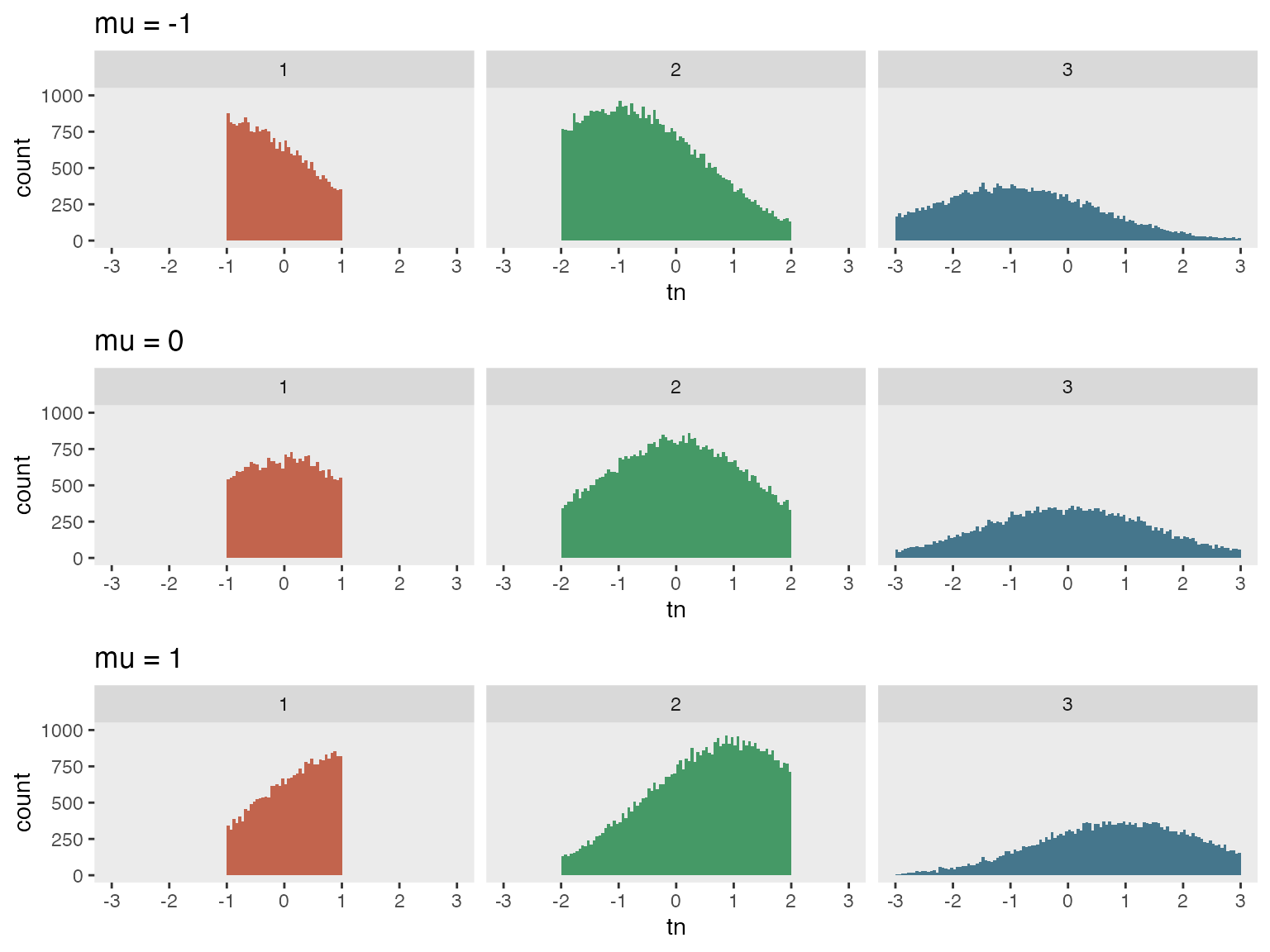
In this second example, we are generating sets of truncated Gaussian
distributions with means ranging from
to
.
The limits of the truncation vary across three different groups.
rnormt is a customized (user-defined) function that
generates the truncated Gaussiandata. The function requires four
arguments (the left truncation value, the right truncation value, the
distribution average and the standard deviation).
rnormt <- function(n, min, max, mu, s) {
F.a <- pnorm(min, mean = mu, sd = s)
F.b <- pnorm(max, mean = mu, sd = s)
u <- runif(n, min = F.a, max = F.b)
qnorm(u, mean = mu, sd = s)
}In this example, truncation limits vary based on group membership. Initially, three groups are created, followed by the generation of truncated values. For Group 1, truncation occurs within the range of to , for Group 2, it’s to and for Group 3, it’s to . We’ll generate three data sets, each with a distinct mean denoted by M, using the double-dot notation to implement these different means.
def <-
defData(
varname = "limit",
formula = "1/4;1/2;1/4",
dist = "categorical"
) |>
defData(
varname = "tn",
formula = "rnormt",
variance = "min = -limit, max = limit, mu = ..M, s = 1.5",
dist = "custom"
)The data generation requires three calls to genData. The
output is a list of three data sets:
Here are the first six observations from each of the three data sets:
## [[1]]
## Key: <id>
## id limit tn
## <int> <int> <num>
## 1: 1 2 0.6949619
## 2: 2 2 -0.3641963
## 3: 3 2 -0.4721632
## 4: 4 3 -2.6083796
## 5: 5 2 -0.6800441
## 6: 6 3 -0.5813880
##
## [[2]]
## Key: <id>
## id limit tn
## <int> <int> <num>
## 1: 1 1 0.4853614
## 2: 2 2 -0.5690811
## 3: 3 2 0.5282246
## 4: 4 2 0.1107778
## 5: 5 2 -0.3504309
## 6: 6 2 1.9439890
##
## [[3]]
## Key: <id>
## id limit tn
## <int> <int> <num>
## 1: 1 2 1.3560628
## 2: 2 2 1.4543616
## 3: 3 3 1.4491010
## 4: 4 2 0.7328855
## 5: 5 2 -0.1254556
## 6: 6 2 -0.7455908A plot highlights the group differences.