Simulating Study Data • simstudy

The simstudy package is a collection of functions that allows users to generate simulated data sets to explore modeling techniques or better understand data generating processes. The user defines the distributions of individual variables, specifies relationships between covariates and outcomes, and generates data based on these specifications. The final data sets can represent randomized control trials, repeated measure designs, cluster-randomized trials, or naturally observed data processes. Other complexities that can be added include survival data, correlated data, factorial study designs, step wedge designs, and missing data processes.

Simulation using simstudy has two fundamental steps. The user (1) defines the data elements of a data set and (2) generates the data based on these definitions. Additional functionality exists to simulate observed or randomized treatment assignment/exposures, to create longitudinal/panel data, to create multi-level/hierarchical data, to create data sets with correlated variables based on a specified covariance structure, to merge data sets, to create data sets with missing data, and to create non-linear relationships with underlying spline curves.

The overarching philosophy of simstudy is to create data generating processes that mimic the typical models used to fit those types of data. So, the parameterization of some of the data generating processes may not follow the standard parameterizations for the specific distributions. For example, in simstudy gamma-distributed data are generated based on the specification of a mean $\mu$ (or $\log(\mu)$ ) and a dispersion $d$ , rather than shape $\alpha$ and rate $\beta$ parameters that more typically characterize the gamma distribution. When we estimate the parameters, we are modeling $\mu$ (or some function of $(\mu)$ ), so we should explicitly recover the simstudy parameters used to generate the model - illuminating the relationship between the underlying data generating processes and the models.

Overview

This introduction provides a brief overview to the basics of defining and generating data, including treatment or exposure variables. Subsequent sections in this vignette provide more details on these processes. For information on more elaborate data generating mechanisms, please refer to other vignettes in this package that provide more detailed descriptions.

Defining the Data

The key to simulating data in simstudy is the creation of a series of data definition tables that look like this:

varname	formula	variance	dist	link
age	10	2	normal	identity
female	-2 + age * 0.1	0	binary	logit
visits	1.5 - 0.2 * age + 0.5 * female	0	poisson	log

These definition tables can be generated in two ways. One option is to use any external editor that allows the creation of .csv files, which can be read in with a call to defRead. An alternative is to make repeated calls to the function defData. This script builds a definition table internally:

def <- defData(varname = "age", dist = "normal", formula = 10,
    variance = 2)
def <- defData(def, varname = "female", dist = "binary",
    formula = "-2 + age * 0.1", link = "logit")
def <- defData(def, varname = "visits", dist = "poisson",
    formula = "1.5 - 0.2 * age + 0.5 * female", link = "log")

The data definition table includes a row for each variable that is to be generated, and has the following fields: varname*, formula, variance, dist, and link. varname provides the name of the variable to be generated. formula is either a value or string representing any valid R formula (which can include function calls) that in most cases defines the mean of the distribution. variance is a value or string that specifies either the variance or other parameter that characterizes the distribution; the default is 0. dist is defines the distribution of the variable to be generated; the default is normal. The link is a function that defines the relationship of the formula with the mean value, and can either identity, log, or logit, depending on the distribution; the default is identity.

If using defData to create the definition table, the first call to defData without specifying a definition name (in this example the definition name is def) creates a new data.table with a single row. An additional row is added to the table def each time the function defData is called. Each of these calls is the definition of a new field in the data set that will be generated.

Generating the data

After the data set definitions have been created, a new data set with $n$ observations can be created with a call to function genData. In this example, 1,000 observations are generated using the data set definitions in def, and then stored in the object dd:

set.seed(87261)

dd <- genData(1000, def)
dd

## Key: <id>
##          id   age female visits
##       <int> <num>  <int>  <int>
##    1:     1  9.78      0      0
##    2:     2 10.81      0      0
##    3:     3  8.86      0      1
##    4:     4  9.83      1      1
##    5:     5 10.58      0      0
##   ---                          
##  996:   996  8.87      1      2
##  997:   997 10.27      0      0
##  998:   998  6.84      0      1
##  999:   999  9.28      0      2
## 1000:  1000 10.80      1      2

If no data definition is provided, a simple data set is created with just id’s.

genData(1000)

## Key: <id>
##          id
##       <int>
##    1:     1
##    2:     2
##    3:     3
##    4:     4
##    5:     5
##   ---      
##  996:   996
##  997:   997
##  998:   998
##  999:   999
## 1000:  1000

Assigning treatment/exposure

In many instances, the data generation process will involve a treatment or exposure. While it is possible to generate a treatment or exposure variable directly using the data definition process, trtAssign and trtObserve offer the ability to generate more involved types of study designs. In particular, with trtAssign, balanced and stratified designs are possible.

study1 <- trtAssign(dd, n = 3, balanced = TRUE, strata = c("female"),
    grpName = "rx")
study1

## Key: <id>
##          id   age female visits    rx
##       <int> <num>  <int>  <int> <int>
##    1:     1  9.78      0      0     3
##    2:     2 10.81      0      0     1
##    3:     3  8.86      0      1     3
##    4:     4  9.83      1      1     3
##    5:     5 10.58      0      0     3
##   ---                                
##  996:   996  8.87      1      2     2
##  997:   997 10.27      0      0     3
##  998:   998  6.84      0      1     1
##  999:   999  9.28      0      2     1
## 1000:  1000 10.80      1      2     3

study1[, .N, keyby = .(female, rx)]

## Key: <female, rx>
##    female    rx     N
##     <int> <int> <int>
## 1:      0     1   249
## 2:      0     2   248
## 3:      0     3   248
## 4:      1     1    85
## 5:      1     2    85
## 6:      1     3    85

More details on data definitions

This section elaborates on the data definition process to provide more details on how to create data sets.

Formulas

The data definition table for a new data set is constructed sequentially. As each new row or variable is added, the formula (and in some cases the variance) can refer back to a previously defined variable. The first row by necessity cannot refer to another variable, so the formula must be a specific value (i.e. not a string formula). Starting with the second row, the formula can either be a value or any valid R equation with quotes and can include any variables previously defined.

In the definition we created above, the probability being female is a function of age, which was previously defined. Likewise, the number of visits is a function of both age and female. Since age is the first row in the table, we had to use a scalar to define the mean.

def <- defData(varname = "age", dist = "normal", formula = 10,
    variance = 2)
def <- defData(def, varname = "female", dist = "binary",
    formula = "-2 + age * 0.1", link = "logit")
def <- defData(def, varname = "visits", dist = "poisson",
    formula = "1.5 - 0.2 * age + 0.5 * female", link = "log")

Formulas can include R functions or user-defined functions. Here is an example with a user-defined function myinv and the log function from base R:

myinv <- function(x) {
    1/x
}

def <- defData(varname = "age", formula = 10, variance = 2,
    dist = "normal")
def <- defData(def, varname = "loginvage", formula = "log(myinv(age))",
    variance = 0.1, dist = "normal")

genData(5, def)

## Key: <id>
##       id   age loginvage
##    <int> <num>     <num>
## 1:     1 10.31     -2.58
## 2:     2  7.90     -1.94
## 3:     3  9.83     -1.93
## 4:     4  9.10     -2.42
## 5:     5 10.18     -2.21

Replication is an important aspect of data simulation - it is often very useful to generate data under different sets of assumptions. simstudy facilitates this in at least two different ways. There is function updateDef which allows row by row changes of a data definition table. In this case, we are changing the formula of loginvage in def so that it uses the function log10 instead of log:

def10 <- updateDef(def, changevar = "loginvage", newformula = "log10(myinv(age))")
def10

##      varname           formula variance   dist     link
##       <char>            <char>   <char> <char>   <char>
## 1:       age                10        2 normal identity
## 2: loginvage log10(myinv(age))      0.1 normal identity

genData(5, def10)

## Key: <id>
##       id   age loginvage
##    <int> <num>     <num>
## 1:     1  9.82    -0.338
## 2:     2 10.97    -0.633
## 3:     3 11.79    -1.267
## 4:     4  9.74    -0.882
## 5:     5 10.11    -1.519

A more powerful feature of simstudy that allows for dynamic definition tables is the external reference capability through the double-dot notation. Any variable reference in a formula that is preceded by “..” refers to an externally defined variable:

age_effect <- 3

def <- defData(varname = "age", formula = 10, variance = 2,
    dist = "normal")
def <- defData(def, varname = "agemult", formula = "age * ..age_effect",
    dist = "nonrandom")

def

##    varname            formula variance      dist     link
##     <char>             <char>    <num>    <char>   <char>
## 1:     age                 10        2    normal identity
## 2: agemult age * ..age_effect        0 nonrandom identity

genData(2, def)

## Key: <id>
##       id   age agemult
##    <int> <num>   <num>
## 1:     1  9.69    29.1
## 2:     2  9.63    28.9

But the real power of dynamic definition is seen in the context of iteration over multiple values:

age_effects <- c(0, 5, 10)
list_of_data <- list()

for (i in seq_along(age_effects)) {
    age_effect <- age_effects[i]
    list_of_data[[i]] <- genData(2, def)
}

list_of_data

## [[1]]
## Key: <id>
##       id   age agemult
##    <int> <num>   <num>
## 1:     1  11.4       0
## 2:     2  10.7       0
## 
## [[2]]
## Key: <id>
##       id   age agemult
##    <int> <num>   <num>
## 1:     1  11.3    56.6
## 2:     2  11.2    56.1
## 
## [[3]]
## Key: <id>
##       id   age agemult
##    <int> <num>   <num>
## 1:     1  9.32    93.2
## 2:     2 10.62   106.2

Distributions

The foundation of generating data is the assumptions we make about the distribution of each variable. simstudy provides 15 types of distributions, which are listed in the following table:

name	formula	string/value	format	variance	identity	log	logit
beta	mean	both	-	dispersion	X	-	X
binary	probability	both	-	-	X	X	X
binomial	probability	both	-	# of trials	X	X	X
categorical	probability	string	p_1;p_2;…;p_n	a;b;c	X	-	X
clusterSize	total N	both	-	dispersion	X	-	-
custom	function	string	-	arguments	X	-	-
exponential	mean	both	-	-	X	X	-
gamma	mean	both	-	dispersion	X	X	-
mixture	formula	string	x_1 \| p_1 + … + x_n \| p_n	-	X	-	-
negBinomial	mean	both	-	dispersion	X	X	-
nonrandom	formula	both	-	-	X	-	-
normal	mean	both	-	variance	X	-	-
noZeroPoisson	mean	both	-	-	X	X	-
poisson	mean	both	-	-	X	X	-
trtAssign	ratio	string	r_1;r_2;…;r_n	stratification	X	X	-
uniform	range	string	from ; to	-	X	-	-
uniformInt	range	string	from ; to	-	X	-	-

beta

A beta distribution is a continuous data distribution that takes on values between $0$ and $1$ . The formula specifies the mean $\mu$ (with the ‘identity’ link) or the log-odds of the mean (with the ‘logit’ link). The scalar value in the ‘variance’ represents the dispersion value $d$ . The variance $\sigma^2$ for a beta distributed variable will be $\mu (1- \mu)/(1 + d)$ . Typically, the beta distribution is specified using two shape parameters $\alpha$ and $\beta$ , where $\mu = \alpha/(\alpha + \beta)$ and $\sigma^2 = \alpha\beta/[(\alpha + \beta)^2 (\alpha + \beta + 1)]$ .

binary

A binary distribution is a discrete data distribution that takes values $0$ or $1$ . (It is more conventionally called a Bernoulli distribution, or is a binomial distribution with a single trial $n=1$ .) The formula represents the probability (with the ‘identity’ link), the relative risk (with the ‘log’ link), or the log odds (with the ‘logit’ link) that the variable takes the value of 1. The mean of this distribution is $p$ , and variance $\sigma^2$ is $p(1-p)$ .

binomial

A binomial distribution is a discrete data distribution that represents the count of the number of successes given a number of trials. The formula specifies the probability of success (with the ‘identity’ link), the relative risk (with the ‘log’ link), or the log odds (with the ‘logit’ link) that the variable takes the value of 1. and the variance field is used to specify the number of trials $n$ . Given a value of $p$ , the mean $\mu$ of this distribution is $n*p$ , and the variance $\sigma^2$ is $np(1-p)$ .

categorical

A categorical distribution is a discrete data distribution taking on values from $1$ to $K$ , with each value representing a specific category, and there are $K$ categories. The categories may or may not be ordered. For a categorical variable with $k$ categories, the formula is a string of probabilities that sum to 1, each separated by a semi-colon: $(p_1 ; p_2 ; ... ; p_k)$ . $p_1$ is the probability of the random variable falling in category $1$ , $p_2$ is the probability of category $2$ , etc. The probabilities can be specified as functions of other variables previously defined. The helper function genCatFormula is an easy way to create different probability strings. The link options are identity or logit. The variance field is optional an allows to provide categories other than the default 1...n in the same format as formula: “a;b;c”. Numeric variance Strings (e.g. “50;100;200”) will be converted to numeric when possible. All probabilities will be rounded to 1e12 decimal points to prevent possible rounding errors.

clusterSize

The clusterSize distribution allocates a total sample size N (specified in the formula argument) across the k rows of the data.table such that the sum of the rows equals N. If the dispersion argument is set to 0, the allocation to each row is N/k, with some rows getting an increment of 1 to ensure that the sum is N. It is possible to relax the assumption of balanced cluster sizes by setting dispersion > 0. As the dispersion increases, the variability of cluster sizes across clusters increases.

custom

Custom distributions can be specified in defData and defDataAdd by setting the argument dist to “custom”. When defining a custom distribution, provide the name of the user-defined function as a string in the formula argument. The arguments of the custom function are listed in the variance argument, separated by commas and formatted as “arg_1 = val_form_1, arg_2 = val_form_2, $\dots$ , arg_K = val_form_K”. The arg_k’s represent the names of the arguments passed to the customized function, where $k$ ranges from $1$ to $K$ . Values or formulas can be used for each val_form_k. If formulas are used, ensure that the variables have been previously generated. Double dot notation is available in specifying value_formula_k. One important requirement of the custom function is that the parameter list used to define the function must include an argument”n = n”, but do not include $n$ in the definition as part of defData or defDataAdd.

exponential

An exponential distribution is a continuous data distribution that takes on non-negative values. The formula represents the mean $\theta$ (with the ‘identity’ link) or log of the mean (with the ‘log’ link). The variance argument does not apply to the exponential distribution. The variance $\sigma^2$ is $\theta^2$ .

gamma

A gamma distribution is a continuous data distribution that takes on non-negative values. The formula specifies the mean $\mu$ (with the ‘identity’ link) or the log of the mean (with the ‘log’ link). The variance field represents a dispersion value $d$ . The variance $\sigma^2$ is is $d \mu^2$ .

mixture

The mixture distribution is a mixture of other predefined variables, which can be defined based on any of the other available distributions. The formula is a string structured with a sequence of variables $x_i$ and probabilities $p_i$ : $x_1 | p_1 + … + x_n | p_n$ . All of the $x_i$ ’s are required to have been previously defined, and the probabilities must sum to $1$ (i.e. $\sum_1^n p_i = 1$ ). The result of generating from a mixture is the value $x_i$ with probability $p_i$ . The variance and link fields do not apply to the mixture distribution.

negBinomial

A negative binomial distribution is a discrete data distribution that represents the number of successes that occur in a sequence of Bernoulli trials before a specified number of failures occurs. It is often used to model count data more generally when a Poisson distribution is not considered appropriate; the variance of the negative binomial distribution is larger than the Poisson distribution. The formula specifies the mean $\mu$ or the log of the mean. The variance field represents a dispersion value $d$ . The variance $\sigma^2$ will be $\mu + d\mu^2$ .

nonrandom

Deterministic data can be “generated” using the nonrandom distribution. The formula explicitly represents the value of the variable to be generated, without any uncertainty. The variance and link fields do not apply to nonrandom data generation.

normal

A normal or Gaussian distribution is a continuous data distribution that takes on values between $-\infty$ and $\infty$ . The formula represents the mean $\mu$ and the variance represents $\sigma^2$ . The link field is not applied to the normal distribution.

noZeroPoisson

The noZeroPoisson distribution is a discrete data distribution that takes on positive integers. This is a truncated poisson distribution that excludes $0$ . The formula specifies the parameter $\lambda$ (link is ‘identity’) or log() (link is log). The variance field does not apply to this distribution. The mean $\mu$ of this distribution is $\lambda/(1-e^{-\lambda})$ and the variance $\sigma^2$ is $(\lambda + \lambda^2)/(1-e^{-\lambda}) - \lambda^2/(1-e^{-\lambda})^2$ . We are not typically interested in modeling data drawn from this distribution (except in the case of a hurdle model), but it is useful to generate positive count data where it is not desirable to have any $0$ values.

poisson

The poisson distribution is a discrete data distribution that takes on non-negative integers. The formula specifies the mean $\lambda$ (link is ‘identity’) or log of the mean (link is log). The variance field does not apply to this distribution. The variance $\sigma^2$ is $\lambda$ itself.

trtAssign

The trtAssign distribution is an implementation of the trtAssign functionality in the context of the defData workflow. Sometimes, it might be convenient to assign treatment or group membership while defining other variables. The formula specifies the relative allocation to the different groups. For example three-arm randomization with equal allocation to each arm would be specified as “1;1;1”. The variance field defines the stratification variables, and would be specified as “s_1;s_2” if s_1 and s_2 are the stratification variables. The link field is used to indicate if the allocations should be perfectly balanced; if nothing is specified (and link defaults to identity), the allocation will be balanced; if link is specified to be different from identity, then the allocation will not be balanced.

uniform

A uniform distribution is a continuous data distribution that takes on values from $a$ to $b$ , where $b$ > $a$ , and they both lie anywhere on the real number line. The formula is a string with the format “a;b”, where a and b are scalars or functions of previously defined variables. The variance and link arguments do not apply to the uniform distribution.

uniformInt

A uniform integer distribution is a discrete data distribution that takes on values from $a$ to $b$ , where $b$ > $a$ , and they both lie anywhere on the integer number line. The formula is a string with the format “a;b”, where a and b are scalars or functions of previously defined variables. The variance and link arguments do not apply to the uniform integer distribution.

Generating multiple variables with a single definition

defRepeat allows us to specify multiple versions of a variable based on a single set of distribution assumptions. The function will add nvar variables to the data definition table, each of which will be specified with a single set of distribution assumptions. The names of the variables will be based on the prefix argument and the distribution assumptions are specified as they are in the defData function. Calls to defRepeat can be integrated with calls to defData.

def <- defRepeat(nVars = 4, prefix = "g", formula = "1/3;1/3;1/3",
    variance = 0, dist = "categorical")
def <- defData(def, varname = "a", formula = "1;1", dist = "trtAssign")
def <- defRepeat(def, 3, "b", formula = "5 + a", variance = 3,
    dist = "normal")
def <- defData(def, "y", formula = "0.10", dist = "binary")

def

##    varname     formula variance        dist     link
##     <char>      <char>    <num>      <char>   <char>
## 1:      g1 1/3;1/3;1/3        0 categorical identity
## 2:      g2 1/3;1/3;1/3        0 categorical identity
## 3:      g3 1/3;1/3;1/3        0 categorical identity
## 4:      g4 1/3;1/3;1/3        0 categorical identity
## 5:       a         1;1        0   trtAssign identity
## 6:      b1       5 + a        3      normal identity
## 7:      b2       5 + a        3      normal identity
## 8:      b3       5 + a        3      normal identity
## 9:       y        0.10        0      binary identity

Adding data to an existing data table

Until this point, we have been generating new data sets, building them up from scratch. However, it is often necessary to generate the data in multiple stages so that we would need to add data as we go along. For example, we may have multi-level data with clusters that contain collections of individual observations. The data generation might begin with defining and generating cluster-level variables, followed by the definition and generation of the individual-level data; the individual-level data set would be adding to the cluster-level data set.

defDataAdd/defRepeatAdd/readDataAdd and addColumns

There are several important functions that facilitate the augmentation of data sets. defDataAdd, defRepeatAdd, and readDataAdd are similar to their counterparts defData, defRepeat, and readData, respectively; they create data definition tables that will be used by the function addColumns. The formulas in these “add-ing” functions are permitted to refer to fields that exist in the data set to be augmented, so all variables need not be defined in the current definition able.

d1 <- defData(varname = "x1", formula = 0, variance = 1,
    dist = "normal")
d1 <- defData(d1, varname = "x2", formula = 0.5, dist = "binary")

d2 <- defRepeatAdd(nVars = 2, prefix = "q", formula = "5 + 3*rx",
    variance = 4, dist = "normal")
d2 <- defDataAdd(d2, varname = "y", formula = "-2 + 0.5*x1 + 0.5*x2 + 1*rx",
    dist = "binary", link = "logit")

dd <- genData(5, d1)
dd <- trtAssign(dd, nTrt = 2, grpName = "rx")
dd

## Key: <id>
##       id      x1    x2    rx
##    <int>   <num> <int> <int>
## 1:     1 -1.3230     1     0
## 2:     2 -0.0494     0     1
## 3:     3 -0.4064     1     0
## 4:     4 -0.5562     1     0
## 5:     5 -0.0941     0     1

dd <- addColumns(d2, dd)
dd

## Key: <id>
##       id      x1    x2    rx    q1    q2     y
##    <int>   <num> <int> <int> <num> <num> <int>
## 1:     1 -1.3230     1     0 4.589  5.70     0
## 2:     2 -0.0494     0     1 9.829 11.74     1
## 3:     3 -0.4064     1     0 2.117  4.47     0
## 4:     4 -0.5562     1     0 0.798  3.24     0
## 5:     5 -0.0941     0     1 7.601  6.98     0

defCondition and addCondition

In certain situations, it might be useful to define a data distribution conditional on previously generated data in a way that is more complex than might be easily handled by a single formula. defCondition creates a special table of definitions and the new variable is added to an existing data set by calling addCondition. defCondition specifies a condition argument that will be based on a variable that already exists in the data set. The new variable can take on any simstudy distribution specified with the appropriate formula, variance, and link arguments.

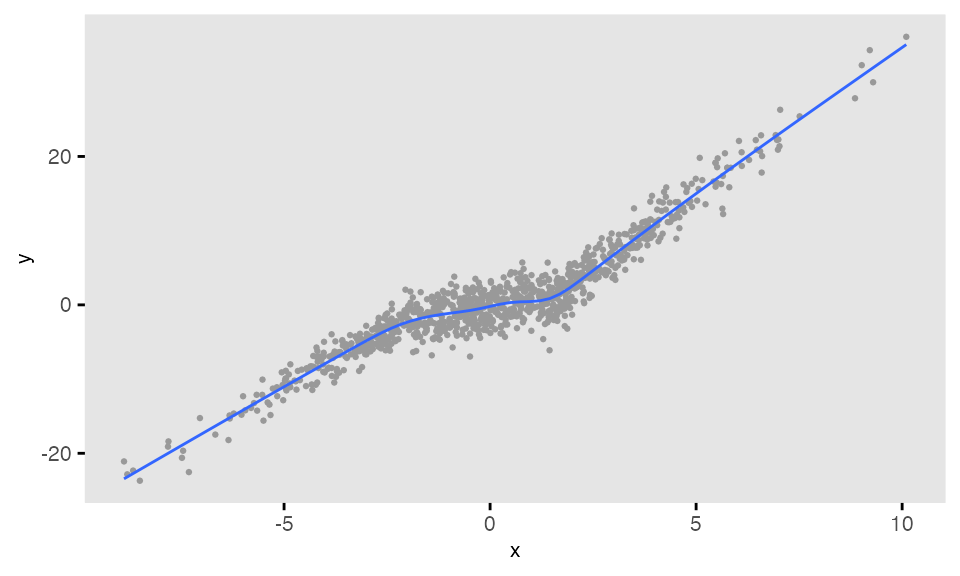
In this example, the slope of a regression line of $y$ on $x$ varies depending on the value of the predictor $x$ :

d <- defData(varname = "x", formula = 0, variance = 9, dist = "normal")

dc <- defCondition(condition = "x <= -2", formula = "4 + 3*x",
    variance = 2, dist = "normal")
dc <- defCondition(dc, condition = "x > -2 & x <= 2", formula = "0 + 1*x",
    variance = 4, dist = "normal")
dc <- defCondition(dc, condition = "x > 2", formula = "-5 + 4*x",
    variance = 3, dist = "normal")

dd <- genData(1000, d)
dd <- addCondition(dc, dd, newvar = "y")

## Warning: Using `size` aesthetic for lines was deprecated in ggplot2 3.4.0.
## ℹ Please use `linewidth` instead.
## This warning is displayed once every 8 hours.
## Call `lifecycle::last_lifecycle_warnings()` to see where this warning was
## generated.